آشنایی با شبکه های پتری و کاربرد های آن
- شبکه پتری
- کابردهای شبکه پتری
- عناصر شبکه پتری
- ساختار شبکه پتری
- مهره ها ( توکن ها )
- تعریف رسمی یک شبکه پتری بصورت ریاضی
- قوانین مربوط به فعال شدن گذارها
- نحوه شکلیک
- انواع اجرا در شبکه پتری
- شبکه های پتری رنگی
- تعريف رسمي شبکههاي پتري رنگي
- ارزيابي رفتار معماری
- تکنیک های ارزيابي رفتار معماری
- تکنیک های ارزيابي رفتار معماري : تعاریف
- مثالی از شبکه پتری در شیمی
- منابع
- مشاهده توضیحات بصورت ویدیویی
شبکه پتری
مطرح شده توسط کارل آدام پتری(Carl Adam Petri) در سال 1962
دکتر کارل آدام پتری ریاضیدان و دانشمند علوم کامپیوتر آلمانی بود . او در سال ۱۹۲۶ در لایپزیک به دنیا آمد و در سال ۲۰۱۰ درگذشت.
درحالی که وی تنها ۱۳ سال سن داشت توانست مفهوم جدیدی از نوعی شبکه را ارئه نماید که برای تحلیل واکنشهای شیمیایی بکار می رفت ، این مفهوم بعد ها به نام شبکه پتری معروف گردید.
فعالیت های دکتر پتری کمک بسیار زیادی به پیشبرد علوم کامپیوتر و گردازش موازی و همچنین محاسبات توزیع شده کرده است.
 Carl Adam Petri
Carl Adam Petri
این مدل شبیه به نمودارهای انتقال حالت STD (State Transition Diagram) می باشد که می تواند سیستم های پیچیده را به سیستم ساده تبدیل نماید.
کابردهای شبکه پتری
کاربرد در مسائل صنعتی :
- بهینه سازی سیستم ها مانند هم روندی
- اشتراک منابع
- کنترل ویژگی های سیستم
- شناسایی فرآیند های تکراری
- فرموله کردن و آنالیز فرآیند ها
- سیستم های بلادرنگ
- مدل سازی خطوط تولید
- سیستم های کنترل خطی
- اعتبار سنجی سیستم های نرم افزاری بزرگ
- تحلیل شبکه های ارتباطی
- مسائل زمان بندی شده صنعتی Timed Petri nets

در ادامه به برخی دیگر از کاربرد های شبکه های پتری می پردازیم
- مدل سازی نرم افزارهای توزیع شده
- عیب یابی و رفع اشکال سیستم های خبره و هوشمند
- کنترل پردازش های گسسته
- سیستم های عامل
- شبکه های عصبی
- پردازش اطلاعات در شبکه های اجتماعی
عناصر شبکه پتری
شبكه پتري ، يك نوع گراف دو گره اي چندگانه می باشد :
گره هاي شبكه هاي پتري عبارتند از:
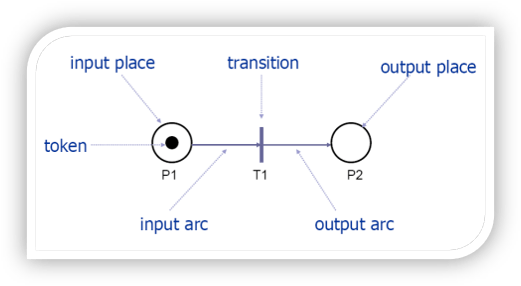
- گره دايره يا مكان Place
- گره ميله يا انتقال Transition
از كمان هاي جهت دار به منظوراتصال مكان ها ( دایره ) به انتقال ها ( میله ) و بر عکس آن استفاده ميشود.
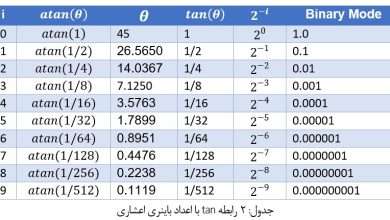
هر شبكه پتري داراي چهار عنصر مدلسازي است :
- انتقال (Transition)
- كمان (Arc)
- مكان (Place)
- مهره (Token)
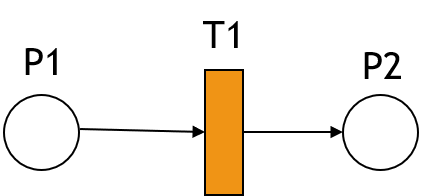
ساختار شبکه پتری
چهار جزء ساختار پتری شامل : C(P,T,I,O)
P: مجموعه مکان های شبکه
T: مجموعه گذارهای شبکه
I: مجموعه توابع ورودی برای گذارهای شبکه
O: مجموعه توابع ورودی برای گذارهای شبکه
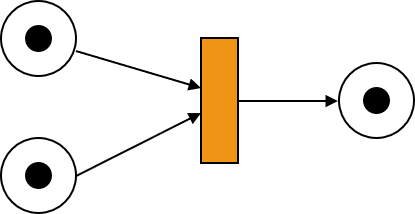
مهره ها ( توکن ها ) در شبکه
- تعداد مهره ها در شبکه با استفاده از تابع M که بصورت یک بردار بازنمایی می شود که در واقع نشان دهنده تعداد مهرهها در هر مکان از شبکه است .
- به تعداد مهرهها در شبکه ، Marking یا علامتگذاري ميگويند.
- به تابع M0 ، علامتگذاري اوليه ميگويند.
- زماني که يک انتقال (آتش ) روی می دهد ، ممکن است علامتگذاري شبکه و در واقع تابع M تغيير می کند.
فرمت کلی تابع M بصورت ذیل می باشد که در آن هر درایه تعداد توکن در هر مکان را مشخص می کند.
M (P) = [a1,a2,…am]
به عنوان مثال در شبکه پتری زیر Marking بصورت ذیل می باشد :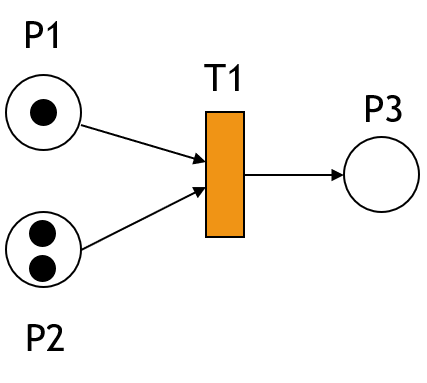
M (P) = [1,2,0]
یک شبکه پتری بصورت ریاضی بدین صورت تعریف می شود :
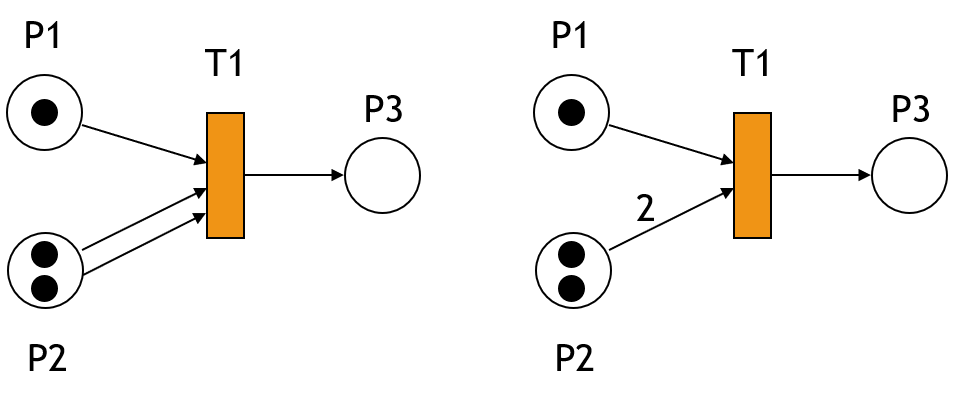
I (P2,T1) = 2
O (T1,P3) = 1
PN = (P, T, I, O, M0)
P = {p1, p2, … pn}
T = {t1, t2, … tn}
Input Function : I = (P * T) à N
Output Function : O = (P * T) à N
M (P) = [a1,a2,…am]
قوانین مربوط به فعال شدن گذارها ( انتقال ها )
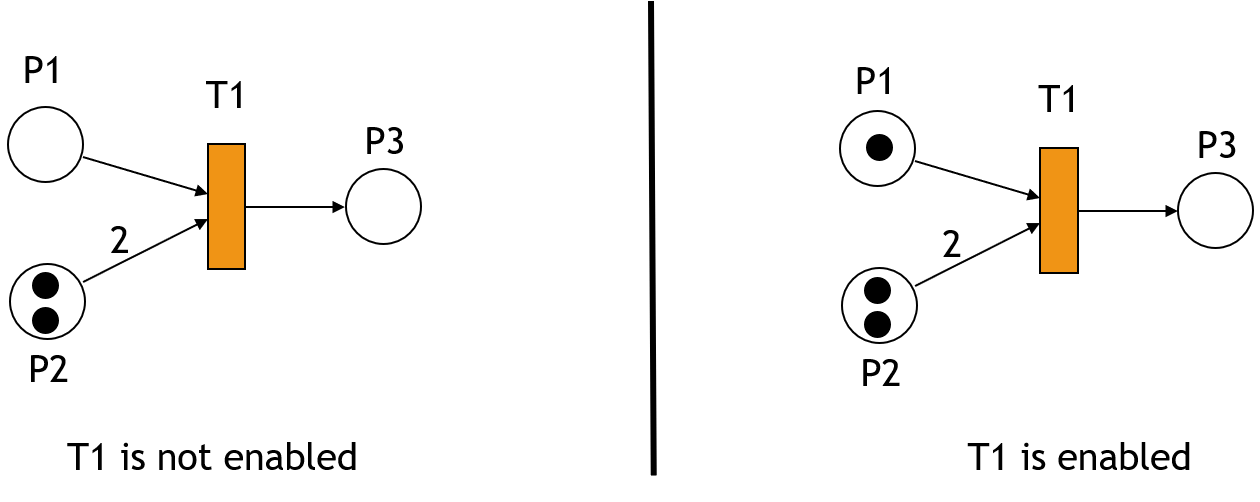
- برای فعال شدن گذارها باید در مکان ما قبل آن حداقل به تعداد ورودی انتقال ( کمان ها ) ، مهره یا TOKEN داشته باشیم.
- به تعداد درجه خروجی از هر گذر TOKEN وارد مکان بعد از انتقال می شود.
- اگر به تعداد خروجی از هر مکان توکن نداشته باشیم گراف مسدود می شود.
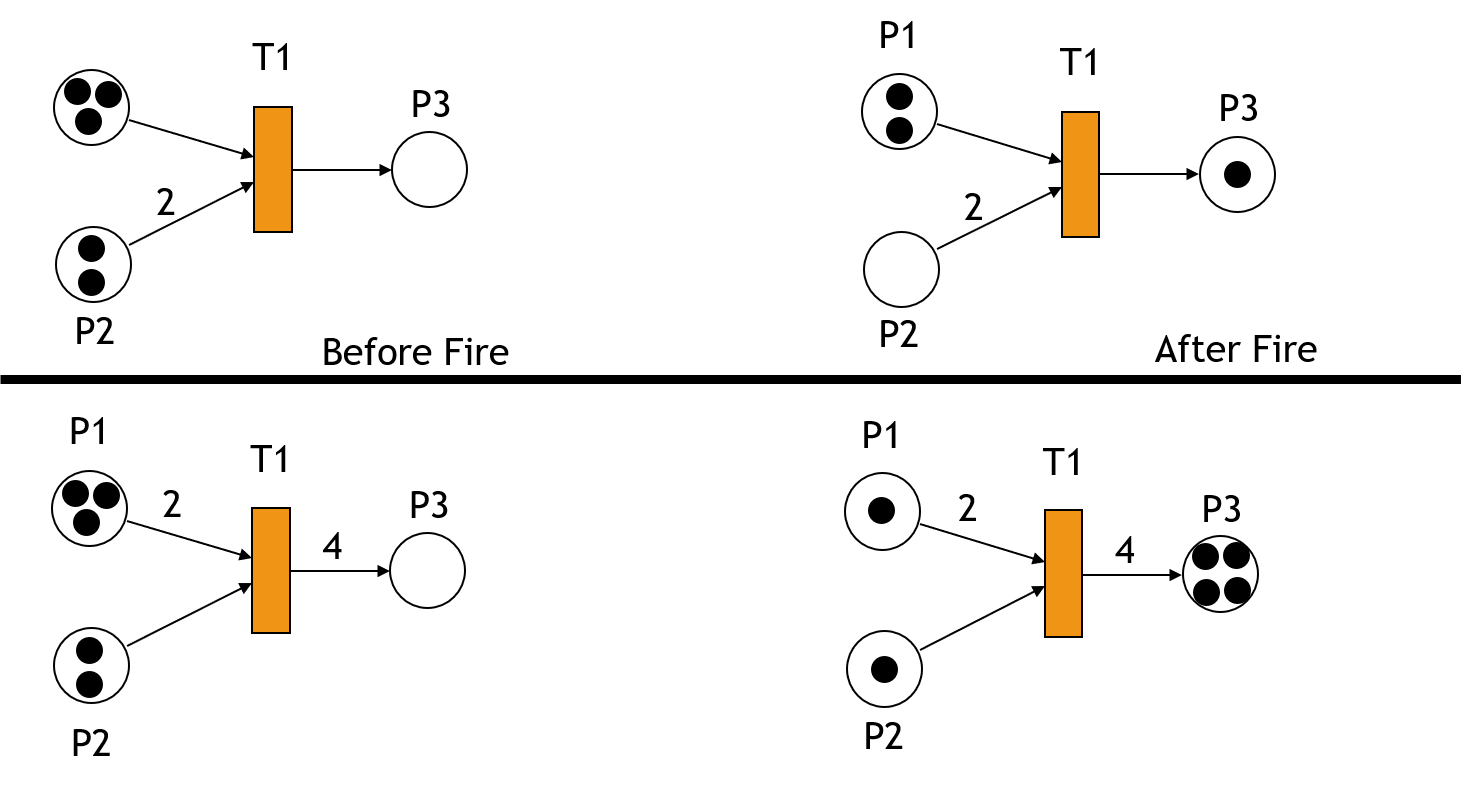
مثال فعال شدن گذار ها ( انتقال ها ) :
شلیک Firing
انواع اجرا در شبکه پتری
اجرای متوالی:
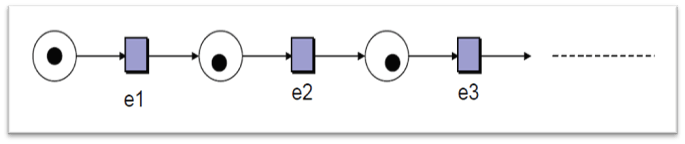
اجرای همروند:
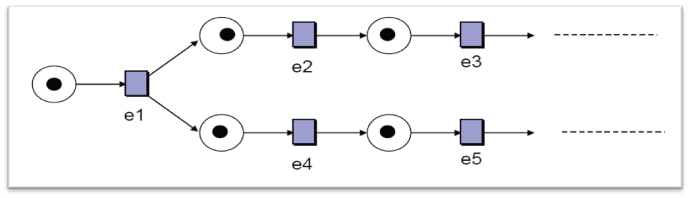
اجرای شانسی : رویدادهای غیر قابل تصمیم گیری:
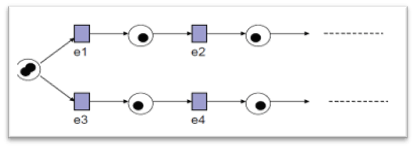
اجرای همزمانی :
اجرای همزمانی و همروندی :
شبکه های پتری رنگی
این نوع از شبکه های پتری حالت كليتري از شبكههاي پترينت معمولي محسوب ميشوند که مدلسازي دقيق تر و جزئيتري را از فرآيندهاي غيرهمزمان و پيچيده را ممکن می سازند. مهرهها ميتوانند با هم متفاوت باشند، بطوريكه به هر مهره خصوصيتي بنام رنگ اضافه ميشود، مهره ها كمانها ميتوانند شامل عبارات رياضي باشند كه از تركيب مجموعه هاي رنگ و متغيرهاي مربوط به آنها تشكيل مي شوند.
متغيرها به منظور قابليت انعطاف بيشتر در مدلسازي سيستم معرفي ميشوند، يک گارد، يک عبارت بولي است که به يک انتقال منتسب ميشود و شرايط بيشتري براي فعال کردن، روي متغيرها در عبارت کمان ورودي اضافه ميکند.
بخش کد يک تکه کد است که با يک انتقال همراه ميشود و زمانيکه انتقال آتش ميشود، کد مذکور اجرا ميشود.
تعريف رسمي شبکههاي پتري رنگي
يک ششتايي مرتب به شکل (P,T,C,I-,I+,M0) است که:
- P يک مجموعه متناهي از مکانها است
- T يک مجموعه متناهي از انتقالها است
- P ∩ T = φ
- C، تابع رنگ و نگاشتي از مجموعه P U T به مجموعه غيرتهي است
- I+ ، I- توابع تلاقي پيشرو و پسرو که بر روي P*T تعريف شده است به طوريکه :

- بر روي P تعريف شده و توصيفکننده علامتگذاري اوليه به است نحويکه به ازاي هر p متعلق به P رابطه C(p) є M0(p) برقرار است.
- در شبکههاي پتري رنگي مفهوم زمان از طريق عنصري با نام ساعت سراسري معرفي ميشوند
- مقاديري که اين ساعت اختيار ميکند بيانکننده زمان مدل است
- اين زمان ميتواند يک عدد صحيح باشد که نشانگر زمان گسسته است يا ميتواند يک عدد حقيقي باشد که بيانکننده زمان پيوسته است.
- علاوه بر اينکه ميتوان به هر مهره، مقداري منتسب کرد، ميتوان به هر مهره مقدار زماني داد. به اين مقدار زماني زمانمهر (Timestamp) گفته ميشود.
- زمانمهر بيانگر اولين زمان مدل است که در آن مهره ميتواند مورد استفاده قرار گيرد
- در يک شبکه پتري رنگي مبتني بر زمان، زماني که مهرهها در مکانهاي ورودي يک انتقال موجود هستند و گارد مربوط به انتقال برقرار است، انتقال مورد نظر فعال ميشود
- براي آنکه اين انتقال بتواند آتش شود، لازم است که در حالت آماده باشد
- زماني، انتقال در حالت آماده است که مهرههاي مکانهاي ورودي انتقال کوچکتر و يا مساوي با زمان فعلي باشد
ارزيابي رفتار معماري
با دانستن اينكه مدل پتري قابليت اجرا شدن دارد و قواعد، ساختارها و دادهها با هم كار ميكنند، ارزيابي انجام می پذیرد، ارزيابي رفتار معماري به معني بررسي عملكرد معماري است.
- سوالات مهمي كه ارزيابي رفتار بايد به آن پاسخ دهد:
- آيا خروجيهاي لازم براي هر سناريو توليد ميشوند؟
- آيا اطلاعات در زمان و ترتيب درست در دسترس هستند؟
رفتار يك معماري را ميتوان با نيازمنديهاي مورد انتظار كاربران مقايسه كرد
تکنیک های ارزيابي رفتار معماري
شبيه سازي
- رفتار معماري را ميتوان با اجراي مدل در حالت شبيه سازي، با وروديها و خروجيهاي فرضي ارزيابي نمود
- تحليل به روش فضاي حالت
- شبكههاي پتري رنگي امكان ارزيابي عددي خواص رفتاري را دارند
- با استفاده از اين تكنيك ميتوان به مشكلات معماري نظير بنبستها، حلقههاي بينهايت و غيره پي برده و تعداد مهرههائي كه در هر مكان از شبكه قرار مي گيرند را نيز محاسبه نمود
تکنیک های ارزيابي رفتار معماري : تعاریف
- در يك شبكه پتري، يك « مسير ساده جريان اطلاعات » به هر مسيري كه از يك منبع به يك مقصد منتهي شود اطلاق ميشود
- در هر معماري يكسري عملكردهاي پايه وجود دارند كه عبارتند از دنبالهاي مرتب از توابعي كه در روي يك پيام ورودي عمل كرده و منجر به يك پيام خروجي ميشود
- يك « مسير كامل جريان اطلاعات » به تمام مسيرهاي ساده جريان اطلاعات اطلاق ميشود كه به يك «مقصد» خاص منتهي ميشوند
- از نقطه نظر معماري، هر مسير كامل جريان اطلاعات معادل يك « عملكرد كامل » است كه قادر است يكسري ورودي را دريافت كرده و در نهايت به يك خروجي مشخص تبديل نمايد
- هر مسير ساده جريان اطلاعات، فقط و فقط به يك مسير كامل جريان اطلاعات متعلق است
- روش ايجاد مسيرهاي كامل جريان اطلاعات:
- اقدام به شناسائي مسيرهاي حداقل در روي شبكه پتري نمائيد
- مسيرهاي حداقل را بر حسب «مقصد» گروه بندي كنيد
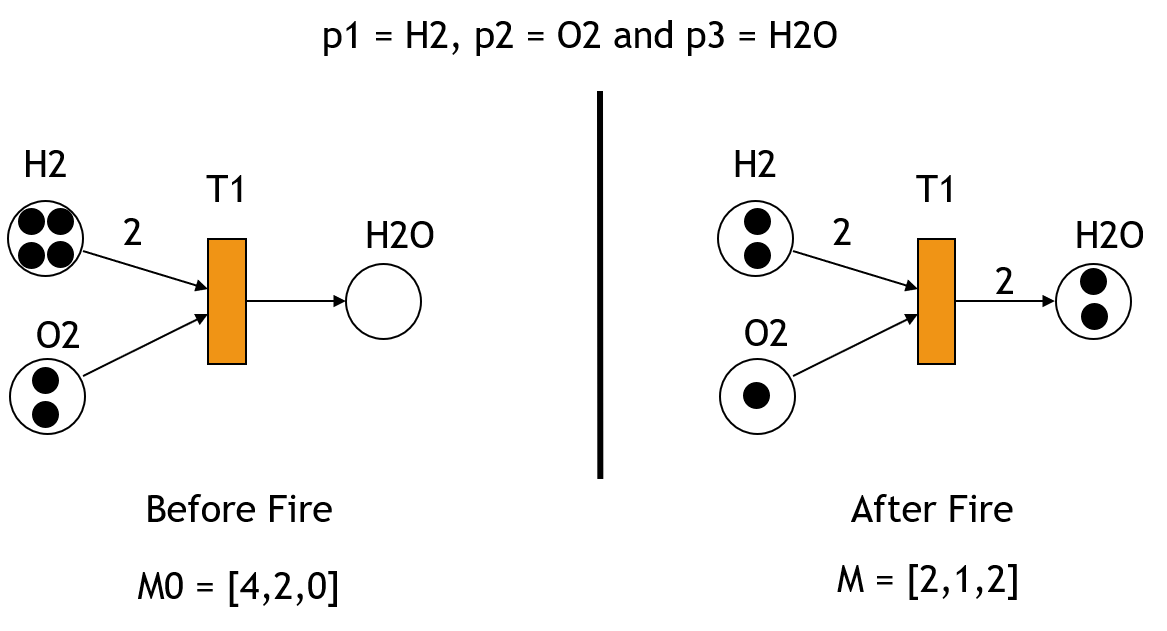
مثالی از شبکه پتری در شیمی
منابع
1.M.o’brien, Petri Nets: “Properties,Application,and Variations“ University of Pittsburg.
2.http://people.cs.pitt.edu/~chang/231/y16/231sem/semObrien.pdf
3.Wikipedia contributors. “Chomsky hierarchy.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 19 Oct. 2016. Web. 19 Oct. 2016